Journal Signal Processing “LCS graph kernel based on Wasserstein distance”
“LCS graph kernel based on Wasserstein distance in longest common subsequence metric space” published on Journal of Signal Processing
Our paper has been accepted into the International Journal of Signal Processing, Elsevier (Impact Factor: 4.662).
-
LCS graph kernel based on Wasserstein distance in longest common subsequence metric space
- Author: J. Huang (M1, 1st-year graduate student when submitting), Z. Fang (B4, 4th-year undergraduate student when submitting), and HK
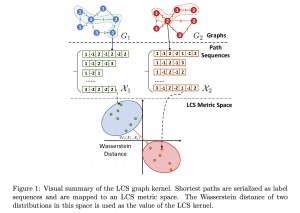
- Abstract: For graph classification tasks, many methods use a common strategy to aggregate information of vertex neighbors. Although this strategy provides an efficient means of extracting graph topological features, it brings excessive amounts of information that might greatly reduce its accuracy when dealing with large-scale neighborhoods. Learning graphs using paths or walks will not suffer from this difficulty, but many have low utilization of each path or walk, which might engender information loss and high computational costs. To solve this, we propose a graph kernel using a longest common subsequence (LCS kernel) to compute more comprehensive similarity between paths and walks, which resolves substructure isomorphism difficulties. We also combine it with optimal transport theory to extract more in-depth features of graphs. Furthermore, we propose an LCS metric space and apply an adjacent point merge operation to reduce its computational costs. Finally, we demonstrate that our proposed method outperforms many state-of-the-art graph kernel methods.
- Information: Volume 189, December 2021, DOI: https://doi.org/10.1016/j.sigpro.2021.108281
- Paper: publisher’s website (free access for 50 days), arXiv preprint arXiv:2012.03612
- Code: GitHub.