Applications of Riemannian optimization
Riemannian joint dimensionality reduction and dictionary learning on symmetric positive definite
Dictionary learning (DL) and dimensionality reduction (DR) are powerful tools for analyzing high-dimensional noisy signals. This paper proposes a novel Riemannian joint dimensionality reduction and dictionary learning (R-JDRDL) on symmetric positive definite (SPD) manifolds for classification tasks. Joint learning considers the interaction between dimensionality reduction and dictionary learning procedures by connecting them into a unified framework. We exploit a Riemannian optimization framework for solving DL and DR problems jointly. Finally, we demonstrate that the proposed Riemannian Joint framework of Dimensionality Reduction and Dictionary Learning, dubbed R-JDRDL, outperforms existing state-of-the-art algorithms when used for image classification tasks.
Given ![]()
![]() , we calculate
, we calculate ![]() ,
, ![]() , and
, and ![]() as
as

where ![]() ,
, ![]() , and
, and ![]() .
.
近年,辞書学習とスパース表現係数を用いた処理手法は,信号処理,画像処理,コンピュータビジョン,パターン認識,機械学習,統計学習等の様々な分野で大きな注目を集めている.しかしながら,対象信号の高次元化に伴い,計算処理量が増大するだけでなく,潜在的構造に寄与する信号が高次元空間の中に埋没し,辞書学習やスパースコーディング処理における性能劣化を引き起こすという問題が指摘されている.本問題に対して次元削減手法は一つの解決手法であるが,高次元データに対して次元削減を行いその後辞書学習や識別処理を行う独立した処理が一般的であるため,後続の処理に対して最適な次元削減と辞書学習が行われないという問題がある.
一方,データ処理で対象となる信号がユークリッド空間に属さず多様体上に分布する場合がある.正定値対称行列により表現されるデータはその一つであるが,近年,機械学習やコンピュータビジョンの様々なタスクにおいて,当該データを用いた処理手法が高い性能を示す結果が多数報告されている.
そこで本研究では,正定値対称行列から構成されるリーマン多様体上に位置する信号を対象として,クラス識別タスクにおける性能向上を目指し,次元削減と辞書学習の統合学習法について提案する.
Publication
- HK and B. Mishra “Riemannian joint dimensionality reduction and dictionary learning on symmetric positive definite,” EUSIPCO, 2018.
Fast optimization algorithm on the complex oblique manifold for hybrid precoding in Millimeter Wave MIMO systems
Hybrid precoding(-beamforming) is the most promising approach to reducing high hardware costs and high power consumption in large-scale millimeter wave (mmWave) MIMO systems. Hybrid precoding combines large-dimensional analog precoding (or beamforming) via phase shifters with lower-dimensional digital baseband precoding.
A maximization problem of spectral efficiency approximately boils down to a minimization problem of the Euclidean distance between the fully digital precoder and the hybrid precoder. This problem is further formulated as a matrix factorization problem of the fully digital precoder with a product of the digital baseband precoder matrix and the analog radio frequency (RF) precoder (or beamforming) matrix. The noteworthy point is that the phase shifters impose additional element-wise unit modulus constraints on the analog RF precoder matrix.
The conventional works suffer from performance loss in spectral efficiency and high complexities of optimization algorithms in terms of iteration and processing time. This paper proposes a new fast optimization algorithm that improves the calculation algorithm of the gradient and avoids the nested-loop architecture of the state-of-the-art algorithm, MO-AltMin. The problem is newly defined as
![]()
![]()
Exhaustive evaluations demonstrate that the proposed algorithm yields comparable or faster processing speed than the state-of-the-art algorithms while keeping spectral efficiency near-optimal.
ミリ波MIMOシステムにおけるハイブリッド・プリコーディングの設計問題に着目し,スペクトル効率の向上を目指す高速最適化手法を提案する.当該問題は,一般に,フルディジタル・プリコーダ行列 ![]() とハイブリッド・プリコーダ行列間の距離の最小化問題として定式化される.ここでは,特に,ディジタル・ベースバンド・プリコーダ行列
とハイブリッド・プリコーダ行列間の距離の最小化問題として定式化される.ここでは,特に,ディジタル・ベースバンド・プリコーダ行列 ![]() とアナログRFプリコーダ(ビーム・フォーミング)行列
とアナログRFプリコーダ(ビーム・フォーミング)行列 ![]() を用いた
を用いた ![]() の行列分解 によるアプローチに着目する.当該問題において従来の複素Oblique多様体 上の最適化手法が直面する高い処理複雑さの問題に対して,繰り返し処理構造の最適化 による収束速度向上と,ベクトル化による大規模行列処理の回避 による処理量削減に基づく高速化手法を提案する.スペクトル効率と処理量に関するシミューレショーン実験から,準最適手法を含む最先端の手法に対する提案手法の優位性を示す.
の行列分解 によるアプローチに着目する.当該問題において従来の複素Oblique多様体 上の最適化手法が直面する高い処理複雑さの問題に対して,繰り返し処理構造の最適化 による収束速度向上と,ベクトル化による大規模行列処理の回避 による処理量削減に基づく高速化手法を提案する.スペクトル効率と処理量に関するシミューレショーン実験から,準最適手法を含む最先端の手法に対する提案手法の優位性を示す.
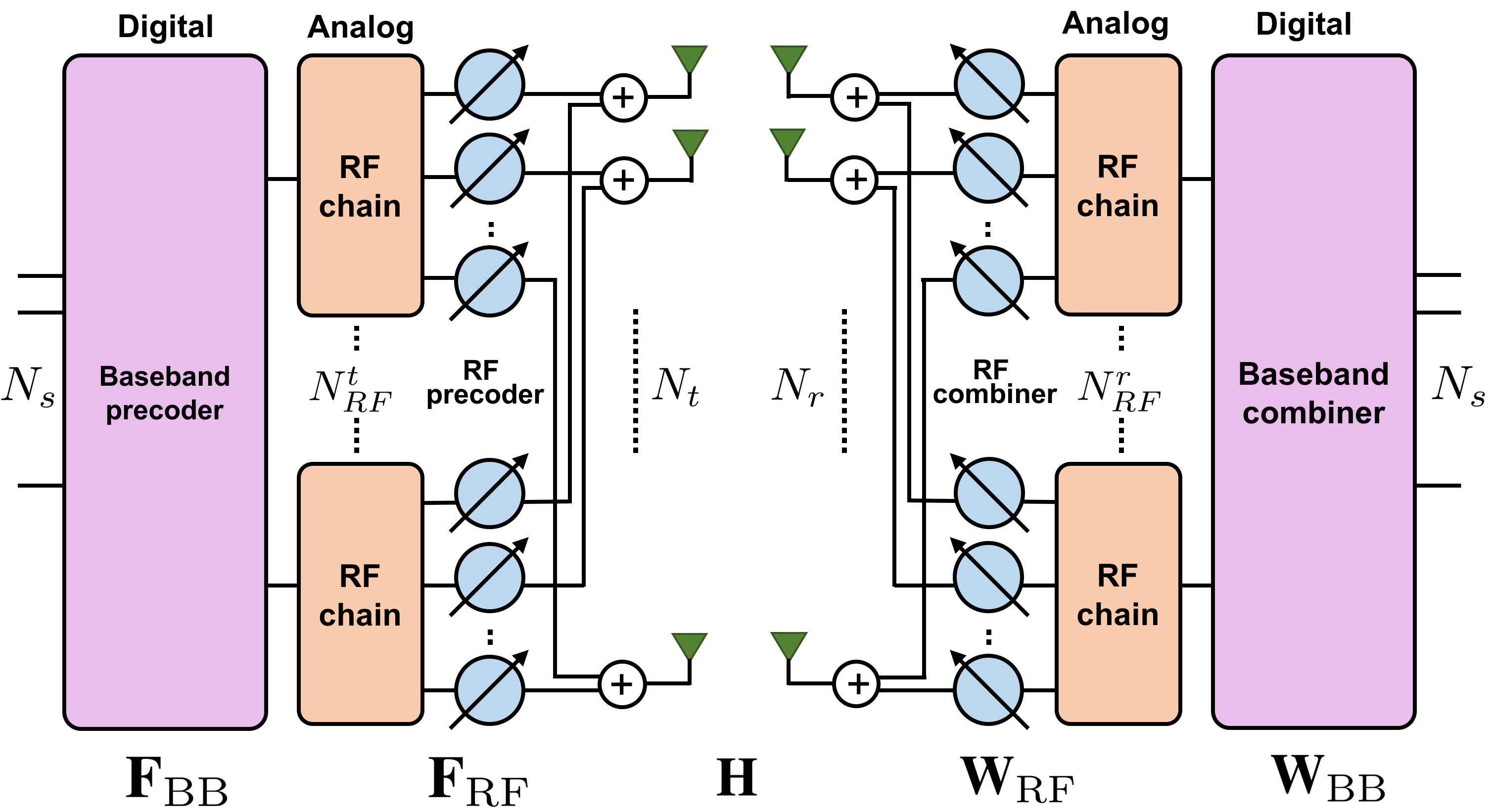
Diagram of hybrid precoder.
Publication
- HK, “Optimization algorithm on the complex oblique manifold for hybrid precoding in Millimeter Wave MIMO systems,” IEEE GlobalSIP, 2018.
The software is available on GitHub.