Riemannian stochastic optimization
Riemannian stochastic gradient descent (R-SGD): an overview
Please see Euclidean stochastic gradient descent algorithm here.
Let ![]() be a smooth real-valued function on a Riemannian manifold
be a smooth real-valued function on a Riemannian manifold ![]() . The target problem concerns a given model variable
. The target problem concerns a given model variable ![]() on
on ![]() , and is expressed as
, and is expressed as
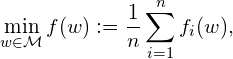
where ![]() is the total number of the elements.
is the total number of the elements.
A popular choice of algorithms for solving this problem is the Riemannian gradient descent method, which calculates the Riemannian full gradient estimation for every iteration. However, this estimation is computationally costly when ![]() is extremely large. A popular alternative is the Riemannian stochastic gradient descent algorithm (R-SGD), which extends the SGD in the Euclidean space to the Riemannian manifold. As R-SGD calculates only one gradient for the
is extremely large. A popular alternative is the Riemannian stochastic gradient descent algorithm (R-SGD), which extends the SGD in the Euclidean space to the Riemannian manifold. As R-SGD calculates only one gradient for the ![]() -th sample, the complexity per iteration is independent of the sample size
-th sample, the complexity per iteration is independent of the sample size ![]() . Although R-SGD requires retraction and vector transport operations in every iteration, those calculation costs can be ignored when they are lower than those of the stochastic gradient; this applies to many important Riemannian optimization problems, including the low-rank tensor completion problem and the Riemannian centroid problem.
. Although R-SGD requires retraction and vector transport operations in every iteration, those calculation costs can be ignored when they are lower than those of the stochastic gradient; this applies to many important Riemannian optimization problems, including the low-rank tensor completion problem and the Riemannian centroid problem.
Accelerated Riemannian SGD
Similarly to SGD, R-SGD is hindered by a slow convergence rate due to a decaying step size sequence. To accelerate the rate of R-SGD, the Riemannian stochastic variance reduced gradient algorithm (R-SVRG) has been proposed; this technique reduces the variance of the stochastic gradient exploiting the finite-sum based on recent progress in variance reduction methods in the Euclidean space. One distinguishing feature is the reduction of the variance of noisy stochastic gradients by periodical full gradient estimations, which yields a linear convergence rate. Riemannian stochastic quasi-Newton algorithm with variance reduction algorithm (R-SQN-VR) has also recently been proposed, where a stochastic quasi-Newton algorithm and the variance reduced methods are mutually combined. Furthermore, the Riemannian stochastic recursive gradient algorithm (R-SRG) has recently been also proposed to accelerate the convergence rate of R-SGD.
Selected publications
- HK, H.Sato and B.Mishra, “Riemannian stochastic recursive gradient algorithm,” ICML2018, poster, (Short version: ICML workshop GiMLi2018).
- HK, H.Sato, and B.Mishra, “Riemannian stochastic quasi-Newton algorithm with variance reduction and its convergence analysis,” AISTATS2018, arXiv2017.
- H.Sato, HK and B.Mishra, “Riemannian stochastic variance reduced gradient algorithm with retraction and vector transport,” SIAM Journal on Optimization, arXiv2017 (Largely extended version of below).
- HK, H.Sato and B.Mishra, “Riemannian stochastic variance reduced gradient on Grassmann manifold,” arXiv2016 and NeurIPS workshop OPT2016 paper.
The code is available here and at Github site. ![]()
Riemannian adaptive stochastic gradient algorithms on matrix manifolds
Besides, a class of algorithms including, for example, Adam, AdaGrad, and RMProp, that has become increasingly common lately, especially in deep learning, adapts the learning rate of each coordinate of the past gradients. However, such explorations on Riemannian manifolds are relatively new and challenging. This is because of the intrinsic nonlinear structure of the underlying manifold and the absence of a canonical coordinate system. In machine learning applications, however, most manifolds of interest form as a matrix with notions of the row and column subspaces. To this end, such a rich structure should not be lost by transforming matrices to just a stack of vectors. For this particular purpose, RASA has been very recently proposed for problems on Riemannian matrix manifolds by adapting the row and column subspaces of gradients.
Publication
- HK, P.Jawanpuria, and B.Mishra, “Riemannian adaptive stochastic gradient algorithms on matrix manifolds,” ICML2019, poser.
Riemannian inexact trust-region algorithm
Riemannian deterministic algorithms such as the Riemannian gradient descent and the Riemannian conjugate gradient descent are first-order algorithms, which guarantee convergence to the first-order optimality condition using only the gradient information. As a result, their performance in ill-conditioned problems suffers due to poor curvature approximation. On the other hand, the Riemannian trust-region algorithm (RTR) comes with a global convergence property, and a superlinear local convergence rate to a second-order optimal point. However, it is computationally prohibitive in a large-scale setting to handle big Hessian matrices. The proposed algorithm approximates the gradient and the Hessian in addition to the solution of a TR sub-problem. Addressing large-scale finite-sum problems, we specifically propose sub-sampled algorithms (Sub-RTR) with a fixed bound on sub-sampled Hessian and gradient sizes, where the gradient and Hessian are computed by a random sampling technique.
Publication
- HK and B.Mishra, “Inexact trust-region algorithms on Riemannian manifolds,” NeurIPS2018 (formerly NIPS), poser.
The code is available at Github site. ![]()
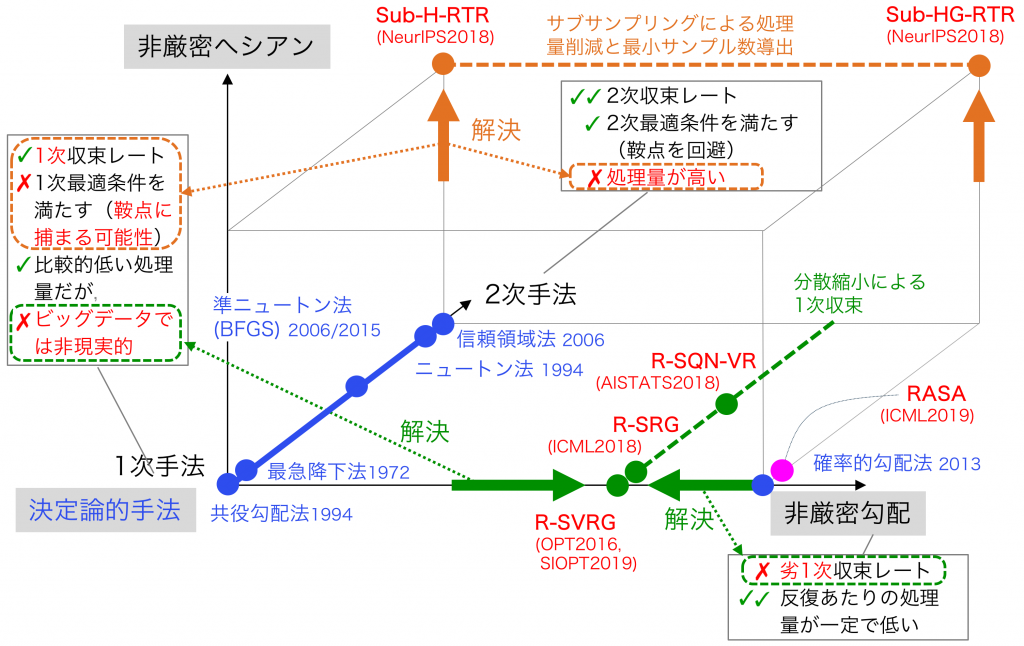
Positioning of proposed algorithms.