Graph analysis
Graph embedding, network embedding
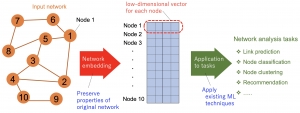
Many practical data systems use network structured data, or graph structured data, which can include web page networks, social networks, road traffic infrastructure, biological networks, and information networks. It is challenging to handle such network data effectively for analytical tasks such as link prediction, node classification, node recommendation, and network visualization. Classical topology-based network representation techniques are hindered by onerous bottlenecks encountered in handling large-scale and high-dimensional network data because they handle an input adjacency matrix directly and because they are adversely affected by noise, outliers, and redundant data. By contrast, network embedding (NE) or graph embedding (GE) has come to be a promising approach that seeks low-dimensional vector representations of nodes in a network to preserve and extract its latent network structure efficiently. Actually, NE alleviates such problems through low-dimensional representation while preserving the original intrinsic structure. Hence, it allows various off-the-shelf machine learning tools to apply this representation directly.
Sequential semi-orthogonal NMF with negative residual reduction (SSO-NRR-NMF)
One recent advanced NE has been achieved in approaches attempting to factorize a given designed matrix to obtain low-dimensional representation assuming that the node connectivity matrix is globally low-rank. It is, however, not always true when the matrix consists of a complex structure. This structure hinders ineffective representations from capturing all the observed connectivity patterns. In this regard, a novel multi-level NE framework (BoostNE) using nonnegative matrix factorizations (NMFs) has been proposed. The framework learns multiple embedding representations with different granularities, i.e., globally and locally low-rankness. However, its sequential multi-level embedding discards negative residuals to enforce residual matrices that are nonnegative at the succeeding level. It also does not consider mutually redundant bases across multiple levels. To alleviate these problems, building on BoostNE, this research presents a proposal of a sequential semi-orthogonal NMF with negative residual reduction, designated as SSO-NRR-NMF. Convergence analysis of SSO-NRR-NMF is also given. Numerical evaluations illustrate the effectiveness of SSO-NRR-NMF when used with several real-world datasets.
Publications
- R. Hashimoto and HK, “Sequential Semi-Orthogonal Multi-Level NMF with Negative Residual Reduction for Network Embedding,” IEEE International Conference on Acoustic, Speech, and Signal Processing (ICASSP) 2020.
Graph matching
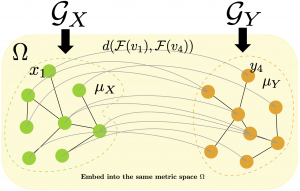
Graph-structured representation has attracted a surge of research interest for the estimation of graph similarity in various graph-based problems. One example representing fundamental problems in machine learning, statistics, and computer vision is graph matching (GM). This problem seeks and aligns optimal correspondence between a pair of graph-structured data to minimize their vertices and edges disagreements. This is a challenging problem in theory and in practice. GM problem arises frequently in many applications including those of computer vision, network analysis, bioinformatics, biology, and data mining. One application is the detection of many variations of malware samples. Coding samples with the graph-structured representation can reformulate such a detection difficulty as a GM difficulty, where unknown samples are compared with already-known malware samples and clean samples. Another application is the graph classification of graph-represented proteins against known proteins in databases, which identifies a new protein obtained in experiments.
The GM problem is generally divided into two categories. The first category is exact graph matching, also known as one-to-one mapping, which requires strict correspondence between the two graphs with the same number of vertices. The second one is, on the other hand, inexact graph matching, also called many-to-many mapping or best graph matching. This process relaxes the requirement of inexact graph matching to allow the merging of multiple vertices to match another one. Therefore, inexact graph matching is applicable to matching between graphs with a different number of vertices.
Publications
-
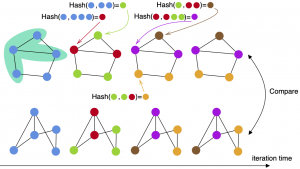
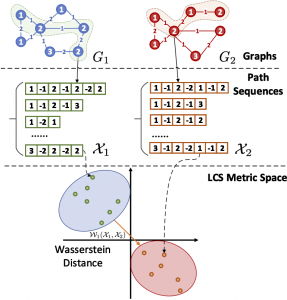
J. Huang, Z. Fang and HK, “LCS graph kernel based on Wasserstein distance in longest common subsequence metric space,” International Journal of Signal Processing, Elsevier (Impact Factor: 4.662), arXiv preprint 2012.03612, 2021.
-
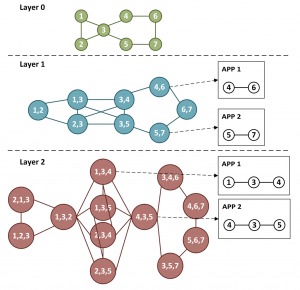
J, Huang and HK, “Graph embedding using multi-layer adjacent point merging model,” IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP) 2021, arXiv preprint 2010.14773, 2020.
Graph-based clustering
Many machine learning applications such as image classification, social networks, chemistry, signal processing, web analysis, item recommendation, and bioinformatics analysis usually exhibit some structured data, which might include trees, groups, clusters, paths, sequences, and graphs. Recent advances in information-retrieval technologies enable the collection of such structured data with heterogeneous features from multi-view data. For example, each web page includes two views of text and images. Image data include multiple features such as color histograms and frequency features of wavelet coefficients. The emergence of such multi-view data has raised a new question: how can such multiple sets of features for individual subjects be integrated into data analysis tasks? This question motivates a new paradigm, called multi-view learning, for data analysis with multi-view feature information. Multi-view learning fundamentally makes use of common or consensus information that is presumed to exist across multi-view data to improve data analysis task performance. One successful subcategory of multi-view learning is multi-view clustering (MVC), which classifies given subjects into subgroups based on similarities among subjects. Although various approaches have been proposed in this category, graph-based multi-view clustering (GMVC) has recently garnered increasing attention: it has demonstrated state-of-the-art performance for numerous applications. Fundamentally, GMVC originates from single-view spectral clustering methods. It performs clustering tasks by exploiting consensus features across input graph matrices such as adjacency matrices. Among them, some works outperform other methods by seeking a consensus matrix called a unified matrix from the input graph matrices with adaptive weights such that the unified matrix directly represents the final clustering result.
Consistency-aware and inconsistency-aware GMVC (CI-GMVC)
Multi-view data analysis has gained increasing popularity because multi-view data are frequently encountered in machine learning applications. A simple but promising approach for clustering multi-view data is multi-view clustering (MVC), which has been developed extensively to classify given subjects into some clustered groups by learning latent common features that are shared across multi-view data. Among existing approaches, graph-based multi-view clustering (GMVC) achieves state-of-the-art performance by leveraging a shared graph matrix called the unified matrix. However, existing methods including GMVC do not explicitly address inconsistent parts of input graph matrices. Consequently, they are adversely affected by unacceptable clustering performance. To this end, this paper proposes a new GMVC method that incorporates consistent and inconsistent parts lying across multiple views.
Publications
- M.Horie and HK, “Consistency-aware and Inconsistency-aware Graph-based Multi-view Clustering,” European Signal Processing Conference (EUSIPCO) 2020. [Publisher site, arXiv preprint: 2011.12532]