Manifold optimization
Optimization on manifolds: an overview
Let ![]() be a smooth real-valued function on a Riemannian manifold
be a smooth real-valued function on a Riemannian manifold ![]() . We consider
. We consider
![]()
where ![]() is a given model variable. This problem has many applications; for example, in principal component analysis (PCA) and the subspace tracking problem, which is the set of
is a given model variable. This problem has many applications; for example, in principal component analysis (PCA) and the subspace tracking problem, which is the set of ![]() -dimensional linear subspaces in
-dimensional linear subspaces in ![]() . The low-rank matrix completion problem and tensor completion problem are promising applications concerning the manifold of fixed-rank matrices/tensors. The linear regression problem is also defined on the manifold of fixed-rank matrices. The independent component analysis (ICA) is an example defined on the oblique manifold.
. The low-rank matrix completion problem and tensor completion problem are promising applications concerning the manifold of fixed-rank matrices/tensors. The linear regression problem is also defined on the manifold of fixed-rank matrices. The independent component analysis (ICA) is an example defined on the oblique manifold.
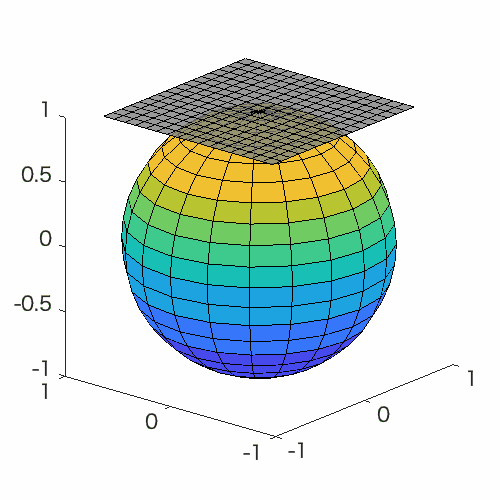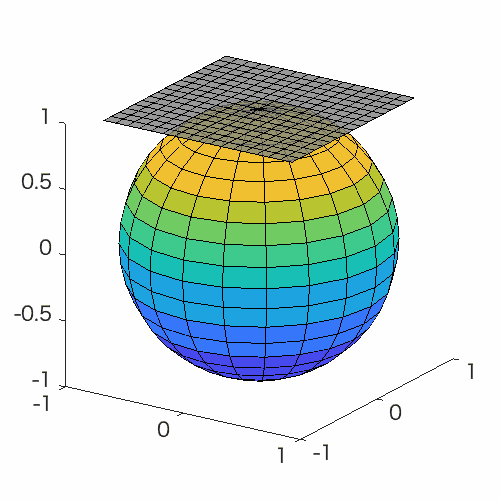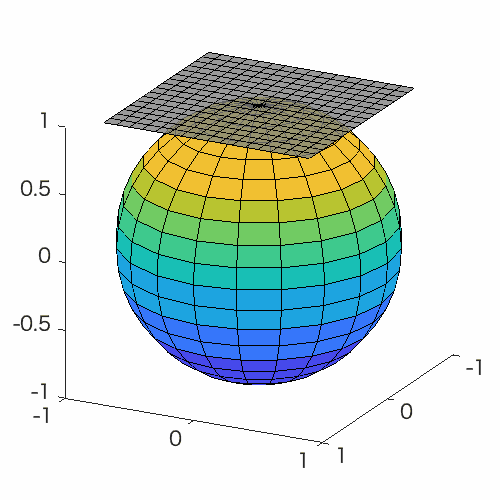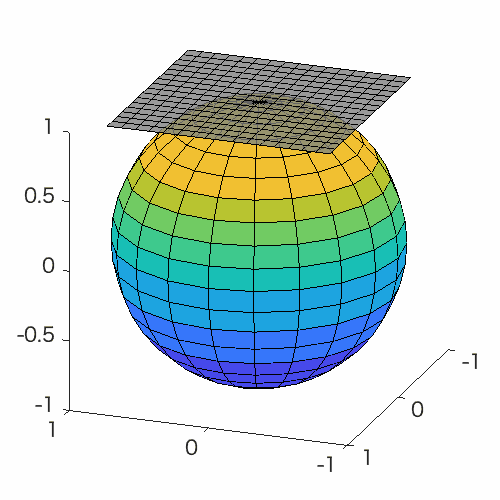
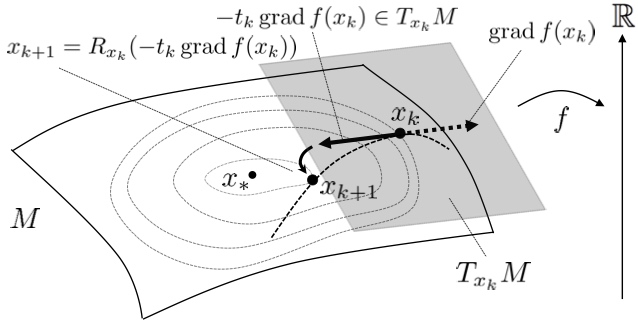
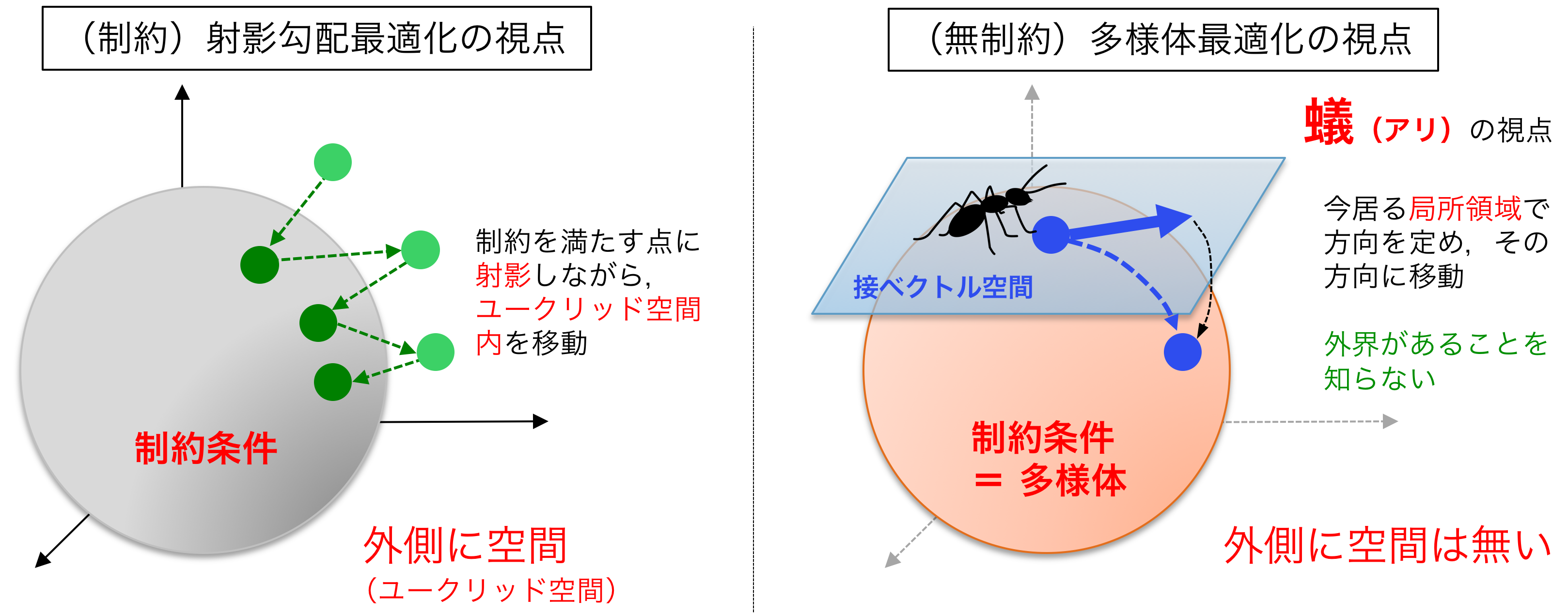
Manifold optimization conceptually translates a constrained optimization problem into an unconstrained optimization problem on a nonlinear search space (manifold). Building upon this point of view, this problem can be solved by Riemannian deterministic algorithms (the Riemannian steepest descent, conjugate gradient descent, quasi-Newton method, Newton’s method, end trust-region (TR) algorithm, etc.) or Riemannian stochastic algorithms.
Publication
- H.Sato and HK, “Optimization on Riemannian Manifolds: Fundamentals and Research Trends,” (in Japanese) Magazine of the Institute of Systems, Control and Information Engineers. 2018.