Stochastic optimization
Stochastic gradient descent
Let ![]() be a smooth real-valued function on
be a smooth real-valued function on ![]() , where
, where ![]() is the dimension. The target problem concerns a given model variable
is the dimension. The target problem concerns a given model variable ![]() , and is expressed as
, and is expressed as
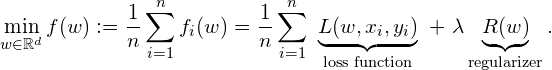
where ![]() represents the model parameter and
represents the model parameter and ![]() denotes the number of samples
denotes the number of samples ![]() .
. ![]() is the loss function and
is the loss function and ![]() is the regularizer with the regularization parameter
is the regularizer with the regularization parameter ![]() . Widely diverse machine learning (ML) models fall into this problem. Considering
. Widely diverse machine learning (ML) models fall into this problem. Considering ![]() ,
, ![]() ,
, ![]() and
and ![]() , this results in
, this results in ![]() -norm regularized linear regression problem (a.k.a. ridge regression) for
-norm regularized linear regression problem (a.k.a. ridge regression) for ![]() training samples
training samples ![]() . In case of the binary classification problem with the desired class label
. In case of the binary classification problem with the desired class label ![]() and
and ![]() ,
, ![]() -norm regularized logistic regression (LR) problem is obtained as
-norm regularized logistic regression (LR) problem is obtained as ![]() , which encourages the sparsity of the solution of
, which encourages the sparsity of the solution of ![]() . Other problems are matrix completion, support vector machines (SVM), and sparse principal components analysis, to name but a few.
. Other problems are matrix completion, support vector machines (SVM), and sparse principal components analysis, to name but a few.
A popular choice of algorithms for solving this problem is the gradient descent method, which calculates the full gradient estimation for every iteration. However, this estimation is computationally costly when ![]() is extremely large. A popular alternative is the the stochastic gradient descent algorithm (SGD). As SGD calculates only one gradient for the
is extremely large. A popular alternative is the the stochastic gradient descent algorithm (SGD). As SGD calculates only one gradient for the ![]() -th sample, the complexity per iteration is independent of the sample size
-th sample, the complexity per iteration is independent of the sample size ![]() .
.
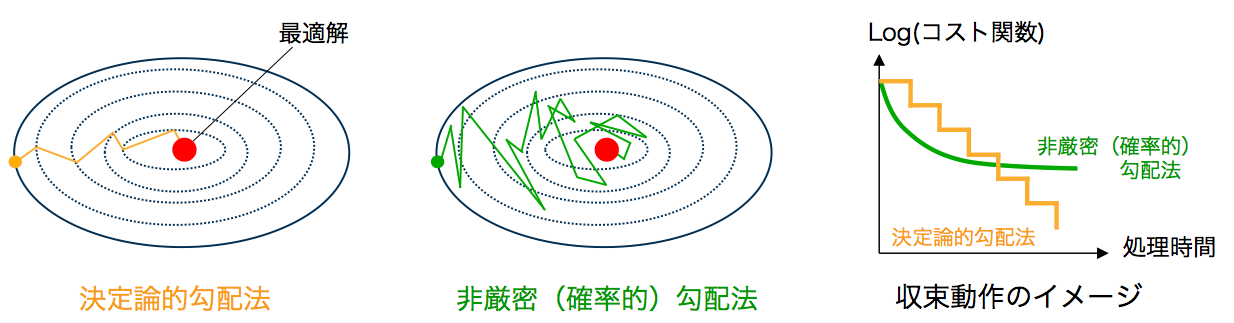
SGD is hindered by a slow convergence rate due to a decaying step size sequence. In addition, the vanilla SGD algorithm is a first-order algorithm, which guarantees convergence to the first-order optimality condition, i.e., ![]() , using only the gradient information. As a result, their performance in ill-conditioned problems suffers due to poor curvature approximation. To address these issues, various advanced techniques have been proposed as below.
, using only the gradient information. As a result, their performance in ill-conditioned problems suffers due to poor curvature approximation. To address these issues, various advanced techniques have been proposed as below.
Recent three techniques for acceleration and improvement
- Variance reduction (VR) techniques to exploit a full gradient estimation to reduce variance of noisy stochastic gradient.
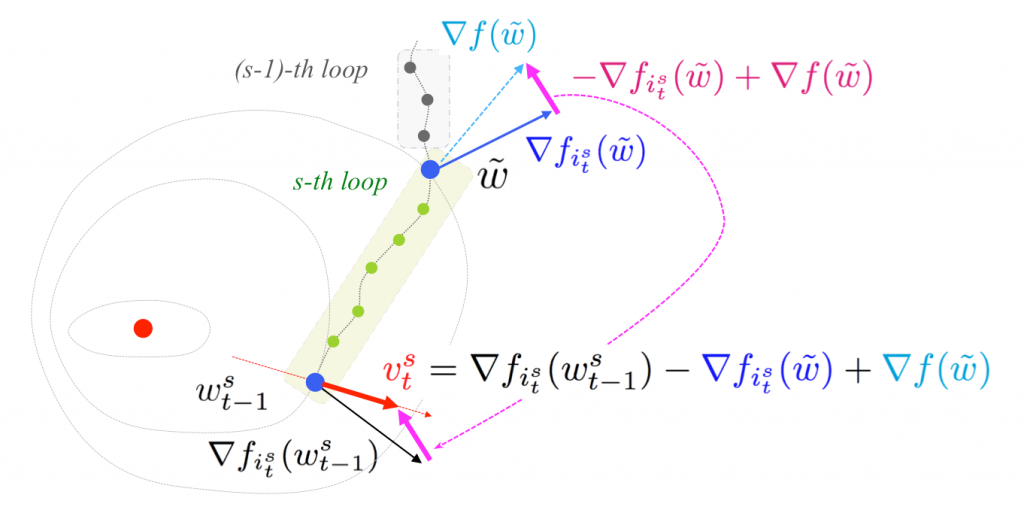
Illustration of stochastic variance reduced gradient (SVRG). SVRG is one representative algorithm of the VR algorithms, which reduces the variance of noisy stochastic gradients by periodical full gradient estimations, which yields a linear convergence rate.
- Second-order (SO) algorithms to solve potential problem of first-order algorithms for ill-conditioned problems.
- Sub-sampled Hessian algorithms to achieve second-order optimality condition.
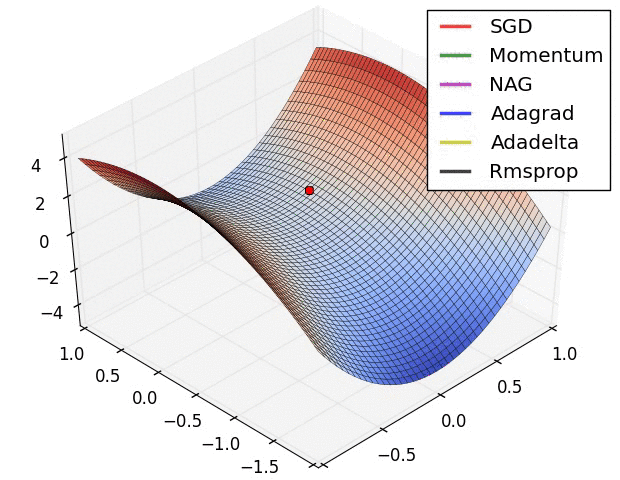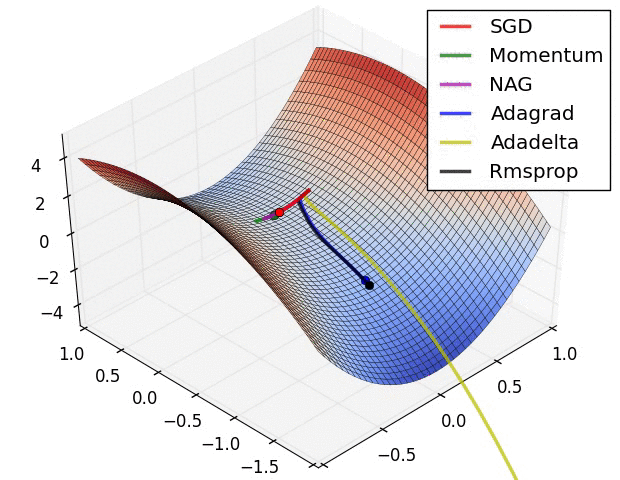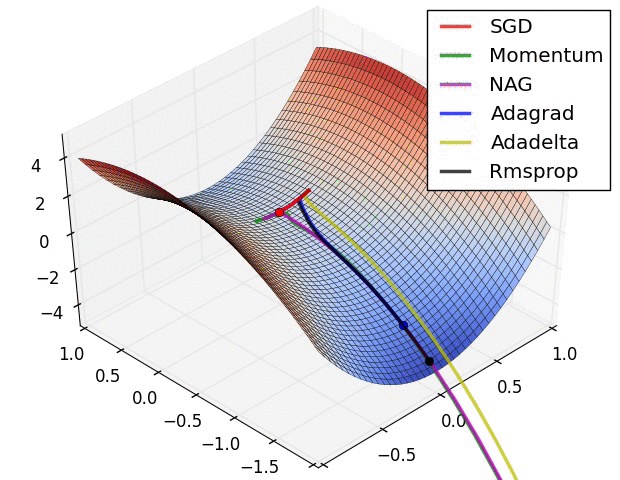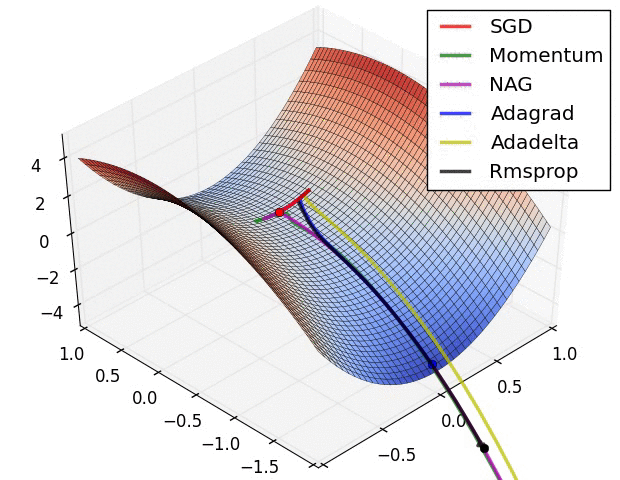
Convergence behavior. (From Sebastian Ruder’s web site)
Software library: SGDLibrary
The SGDLibrary provides a pure-MATLAB library of a collection of stochastic optimization algorithms. Please see the details on software page.
SGDLibrary is on the Github site. ![]()

Publication
- HK, “SGDLibrary: A MATLAB library for stochastic optimization algorithms,” Journal of Machine Learning Research (JMLR) 2018, arXiv2018. (Short version: NIPS workshop MLOSS2018 poster).
Riemannian generalization of stochastic gradient descent
Please see details here.