Multiview learning
Multi-view learning
With advances in information retrieval technologies, many real-world applications such as image classification, item recommendation, web page link analysis, and bioinformatics analysis usually exhibit heterogeneous features from multi-view data. For example, each web page contains two views of text and images with multiple labels. Image data have multiple features such as frequency features of wavelet coefficients and color histograms. The emergence of such multi-view data has raised a new question:
How can we integrate such multiple sets of features for individual subjects in data analysis tasks?
This question motivates a new paradigm in data analysis with multi-view feature information, which is called multi-view learning. Multi-view learning basically makes use of common or consensus information across multi-view data.
Multi-view discriminant learning, one of the supervised learning techniques, has been extensively studied, which generally originates from single-view linear discriminant analysis such as Fisher linear discriminant analysis (LDA or FDA). The general optimization problem is given by
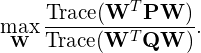
where ![]() and
and ![]() are the matrices describing the interview and intra-view covariances, respectively. Also,
are the matrices describing the interview and intra-view covariances, respectively. Also, ![]() contains the projection matrices of all views, and is defined as
contains the projection matrices of all views, and is defined as
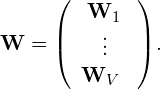
where ![]() is the number of views, and
is the number of views, and ![]() is the projection matrix of the
is the projection matrix of the ![]() -th view. This problem has the form of the Rayleigh quotient, and is reduced to a generalized eigenvalue problem. This category includes, for example, partial least squares (PLS), canonical correlation analysis (CCA), bilinear model (BLM) [9], multi-view discriminant analysis (MvDA), generalized multi-view analysis (GMA)], and standard linear multi-view discriminant analysis (S-LMvDa). Also, MvHE has been proposed to address cases in which the multi-view data are sampled from nonlinear manifolds or where they are adversely affected by heavy outliers.
-th view. This problem has the form of the Rayleigh quotient, and is reduced to a generalized eigenvalue problem. This category includes, for example, partial least squares (PLS), canonical correlation analysis (CCA), bilinear model (BLM) [9], multi-view discriminant analysis (MvDA), generalized multi-view analysis (GMA)], and standard linear multi-view discriminant analysis (S-LMvDa). Also, MvHE has been proposed to address cases in which the multi-view data are sampled from nonlinear manifolds or where they are adversely affected by heavy outliers.
As for unsupervised learning techniques, on the other hand, multi-view clustering (MVC) clusters given subjects into several groups such that the points in the same group are similar and the points in different groups are dissimilar to each other by combining multi-view data. One naive approach of MVC is to perform a single-view clustering method against concatenated features collected from different views. However, this might fail when higher emphases are put to certain specific views than others. Thus, this category of research has attracted more and more attention, which includes multi-view subspace clustering that learns common coefficient matrices, multi-view nonnegative matrix factorization clustering that learns common indicator matrices, multi-view k-means, multi-kernel based multi-view clustering, and CCA based multi-view clustering. Different from the above approaches, graph-based multi-view clustering (GMVC) mainly learns common eigenvector matrices or shared matrices, and empirically demonstrates state-of-the-art results in various applications. The basic steps generally consist of (i) generating an input graph matrix, (ii) generating the graph Laplacian matrix, (iii) computing the embedding matrix, and (iv) performing clustering into groups using an external clustering algorithm. These steps are shared with the normalized cut (Ncut) method and the spectral clustering method. Besides, GMVC is closely related to multi-view spectral clustering.
Publications
- HK, “Multi-view Wasserstein discriminant analysis with entropic regularized Wasserstein distances,” IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 2020, pp. 6039-6043, 2020. [Publisher site]
- M.Horie and HK, “Consistency-aware and Inconsistency-aware Graph-based Multi-view Clustering,” European Signal Processing Conference (EUSIPCO) 2020. [Publisher site, arXiv preprint: 2011.12532]