Riemannian geometry
Tucker tensor manifold with Riemannian metric tuning
We propose a novel preconditioned Tucker manifold for tensor learning problems. A novel Riemannian metric or inner product is proposed that exploits the least-squares structure of the cost function and takes into account the structured symmetry that exists in Tucker decomposition. The specific metric allows to use the versatile framework of Riemannian optimization on quotient manifolds to develop preconditioned nonlinear conjugate gradient and stochastic gradient descent algorithms for batch and online setups, respectively. Concrete matrix representations of various optimization-related ingredients are listed. Numerical comparisons on tensor completion problem and tensor regression problem on forecasting problem suggest that our proposed algorithms robustly outperform state-of-the-art algorithms across different synthetic and real-world datasets.
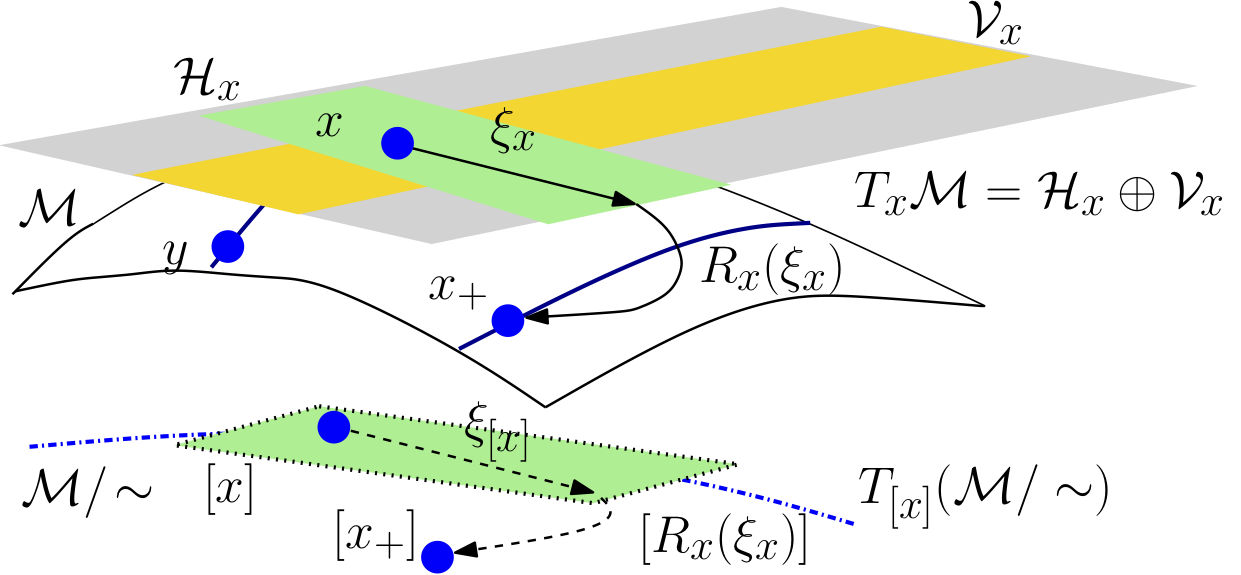
Courtesy of B.Mishra
Applications: tensor regression problem
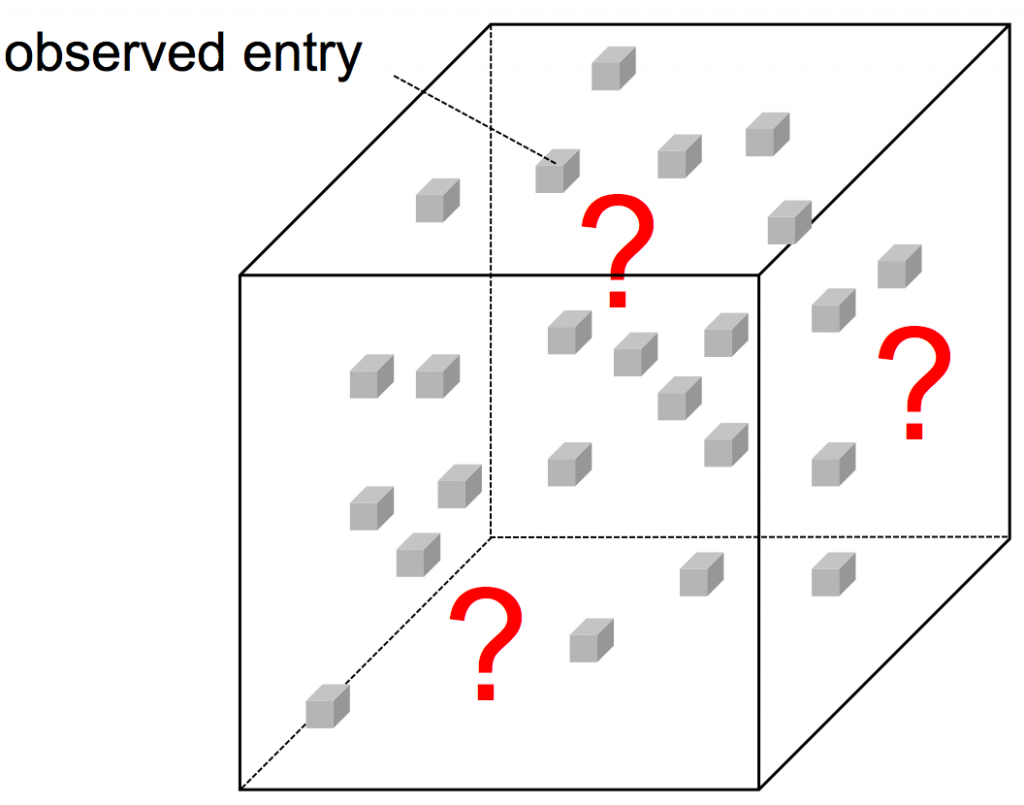
Examples of the tensor regression problem include a tensor completion/decomposition, a higher-order low-rank regression, a multilinear multitask learning, and a spatial-temporal regression. The applications of these problems are, for example, a recommendation problem and spatial-temporal forecasting problem of user/traffic behavior.
We consider the tensor-based regression problem defined as
![]()
where ![]() is the loss function,
is the loss function, ![]() is a coefficient tensor,
is a coefficient tensor, ![]() is input data, and
is input data, and ![]() is a target. We designate a tensor-based regression problem or simply tensor regression problem when the coefficient (the model parameter)
is a target. We designate a tensor-based regression problem or simply tensor regression problem when the coefficient (the model parameter) ![]() has a tensor structure of the order more than three, i.e.,
has a tensor structure of the order more than three, i.e., ![]() . To the contrary,
. To the contrary, ![]() and
and ![]() could be a tensor, a matrix or a vector.
could be a tensor, a matrix or a vector.
Publication
- HK and B.Mishra, “Low-rank tensor completion: a Riemannian manifold preconditioning approach,” ICML2016, arXiv2015 (Short version: NIPS workshop OPT2015).
Simplex of positive definite matrices
We discuss optimization-related ingredients for the Riemannian manifold defined by the constraint
![]()
where the matrix ![]() is symmetric positive definite of size
is symmetric positive definite of size ![]() for all
for all ![]() . For the case
. For the case ![]() , the constraint boils down to the popular standard simplex constraint.
, the constraint boils down to the popular standard simplex constraint.
Publication
- B.Mishra, P.Jawanpuria, and, HK, “Riemannian optimization on the simplex of positive definite matrices,” 12th OPT Workshop on Optimization for Machine Learning at NeurIPS, workshop site, arXiv preprint, 2019.