Manifold optimization Overview

banner-982162_1920

mathematics-1044070_1920

geometry-1023846_1920

lego-1124010_1920

Optimization on manifolds: an overview

Let $f:\mathcal{M} \rightarrow \mathbb{R}$ be a smooth real-valued function on a Riemannian manifold $\mathcal{M}$ . We consider

$\displaystyle{\min_{w \in \mathcal{M}} f(w)},$

where $w \in \mathcal{M}$ is a given model variable. This problem has many applications; for example, in principal component analysis (PCA) and the subspace tracking problem, which is the set of $r$ -dimensional linear subspaces in $\mathbb{R}^d$ , called the Grassmann(ian) manifold. The low-rank matrix completion problem and tensor completion problem are promising applications concerning the manifold of fixed-rank matrices/tensors. The linear regression problem is also defined on the manifold of fixed-rank matrices. The independent component analysis (ICA) is an example defined on the oblique manifold.

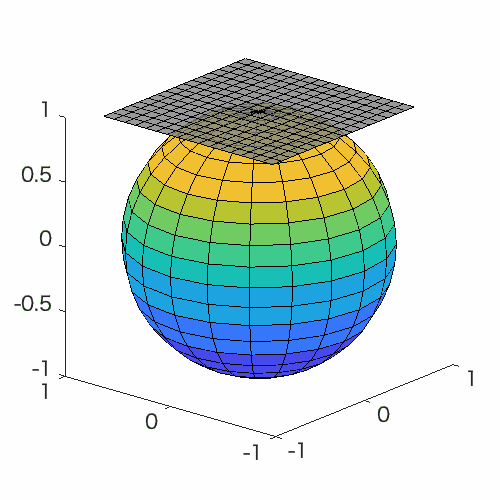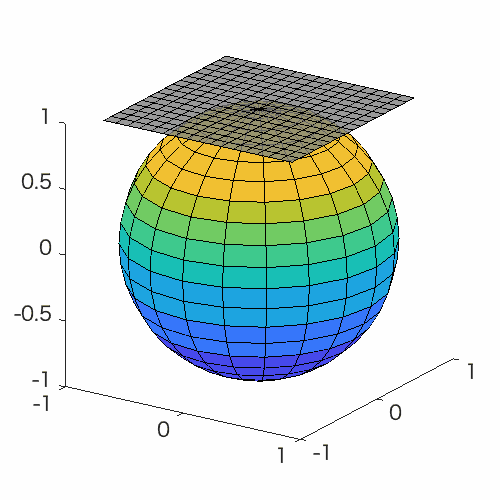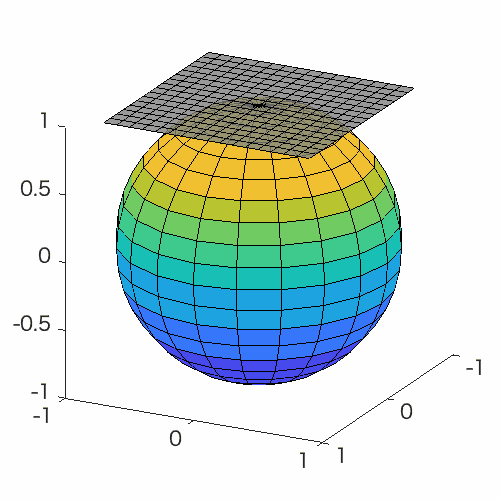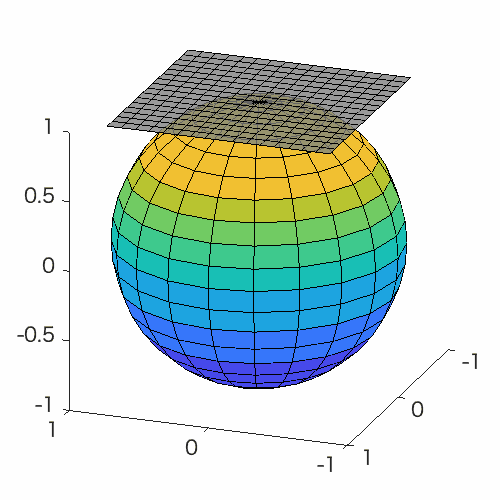
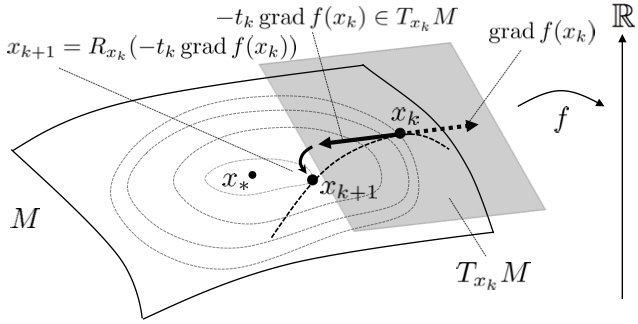
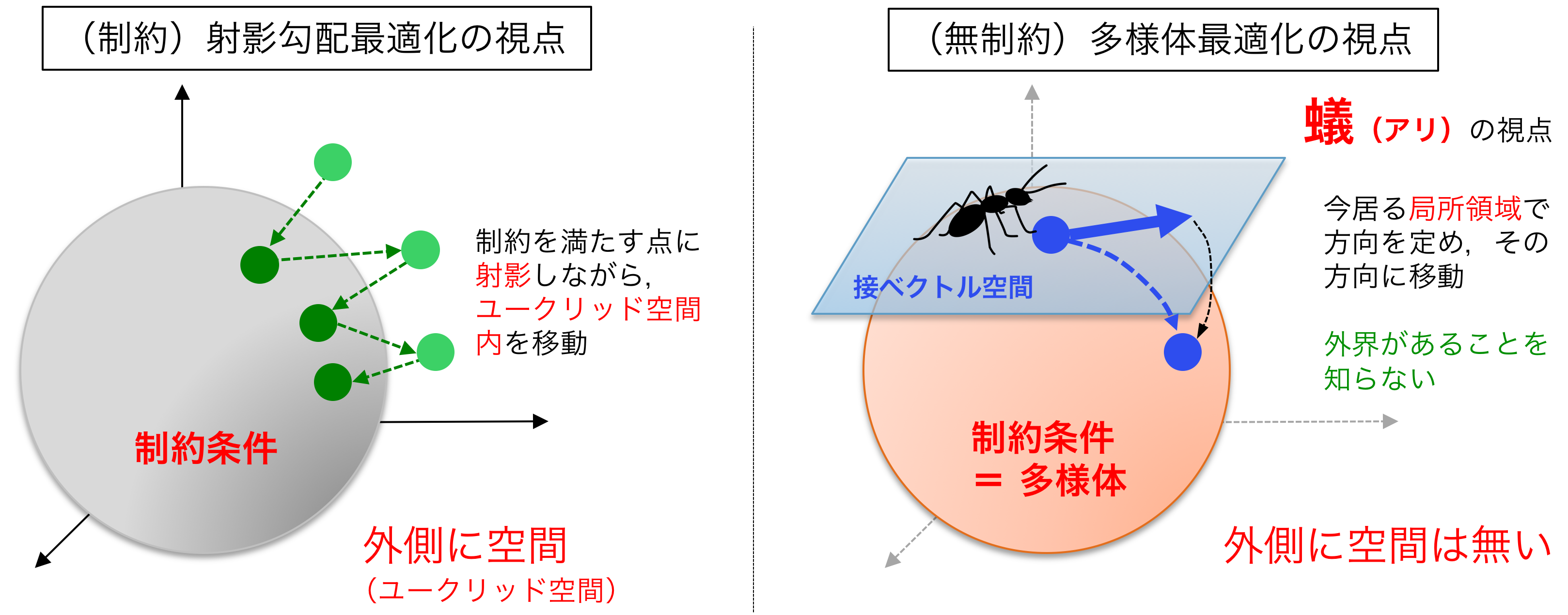
Manifold optimization conceptually translates a constrained optimization problem into an unconstrained optimization problem on a nonlinear search space (manifold). Building upon this point of view, this problem can be solved by Riemannian deterministic algorithms (the Riemannian steepest descent, conjugate gradient descent, quasi-Newton method, Newton’s method, end trust-region (TR) algorithm, etc.) or Riemannian stochastic algorithms.

Publication

H.Sato and HK, “Optimization on Riemannian Manifolds: Fundamentals and Research Trends,” (in Japanese) Magazine of the Institute of Systems, Control and Information Engineers. 2018.

Manifold optimization Overview

Opti­mization on manifolds: an overview

Optimization on manifolds: an overview